2024-02-28
2차 공부 계획
- 2월 25일 - 문제풀이집 1 풀이 (RGB 거리 ~ 오르막 수) 8문제 ✅ 2024-02-26
- 2월 26일 - 문제풀이집 1 풀이 (오르막 수 ~ N과 M 시리즈) 10문제 ✅ 2024-02-26
- 2월 27일 - 문제풀이집 1 완성. (N과 M 시리즈 ~ 끝) 8문제 ✅ 2024-02-27
- 2월 28일 - SW 문제풀이집 2 되는대로 풀기.. 총 70문제 🤯 ✅ 2024-02-28
- 2월 29일 - SW 문제풀이집 2
- 3월 1일 - SW 문제풀이집 2
- 3월 2일 - SW 문제풀이집 2
프로그래머스 알고리즘 고득점 킷 n회독 ?
사람들이 더 하기 싫은 걸 하라고 한다 .. 아니 맞는 말인듯 ..
선 긋기 (2170) - Sweeping Algorithm
라인스위핑 기초 문제. 선 좌표 X, Y가 여러개 주어졌을 때 총 선분 길이를 반환하는 문제다.
Line Sweeping Algorithm은 처음 해봤다. 복잡한 알고리즘보단 아이디어 느낌이라 구현이 어렵진 않았고. 새로운 테크닉을 배운 느낌이다.
공간이나 직선 상에서 한쪽 시작점을 기준으로 반대편 지점까지 스캔 하면서 지나간다, 한번만 스캔해서 지나가면서 마주치는 요소들에 대해 판단기준이 되는 기준을 적용하면서 계산한다.
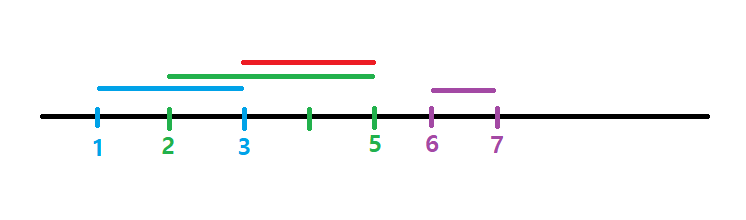
- 선분을 시작점 기준으로 오름차순 정렬한다.
- 시작 지점부터 종료 지점까지 한번만 스캔한다. (가상으로)
- 스캔하면서 각 만나는 요소에 대해 조건을 적용하며 계산한다.
scan_start와 scan_end에 만났던 요소들의 시작 값과 종료 값을 저장해놓고, 선분이 겹치지 않으면 (새 선분이 시작되면) 총 길이를 업데이트 하고(scan_end - scan_start), 선분이 겹치면서 종료값이 초과되면 (그니까 더 현재 선분과 겹치면서 긴 선분을 만나면) scan_end를 늘린다.
#include <algorithm>
#include <iostream>
#include <utility>
#include <vector>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int N;
cin >> N;
vector<pair<int, int>> lines(N);
for (int i = 0; i < N; ++i) {
int start, end;
cin >> lines[i].first >> lines[i].second;
}
sort(lines.begin(), lines.end());
int totalLength = 0;
int scan_start = -1'000'000'000;
int scan_end = -1'000'000'000;
for (const auto &line : lines) {
int start = line.first;
int end = line.second;
if (start > scan_end) { // 선분이 겹치지 않음
totalLength += scan_end - scan_start;
scan_start = start;
scan_end = end;
} else if (end > scan_end) { // 선분 겹침: 초과
scan_end = end;
}
}
// 마지막 선분 고려
totalLength += scan_end - scan_start;
cout << totalLength;
return 0;
}수 묶기 (1744)
수열의 모든 수는 단 한번만 묶거나, 아니면 묶지 않을 수 있다. (묶는다는 것은 서로 곱한다는 것이다)
수열이 주어졌을 때, 수열의 각 수를 적절히 묶었을 때, 그 합이 최대가 되게 하는 프로그램을 작성하는 그리디 + 구현 문제였다.
티어를 가리고 풀었다. BOJ 세팅에서 티어 보기 표시를 해제해서 이제 문제를 맞혀야만 티어를 볼 수 있다.
이걸 해서 좋은 점은 문제의 티어만 보고 쫄지 않는다는 점. 이 문제가 골드 4인걸 알았으면 좀 무서워 했을텐데. 나름 괜찮게 풀었다.
그리디적 해법의 분기가 많아서 구현하는데 약간의 복잡함이 있었다. 문제의 태그도 #많은조건분기 다.
내가 생각한 그리디 분기는 일단..
- 제일 큰 수 두개씩 곱셈한다
- 단, 0과 1이랑은 곱하면 안된다. (더하는 게 더 크다)
- 음수와도 곱하면 안된다.
- 제일 작은 음수 쌍이 있으면 곱한다.
- 음수와 0이 있으면 곱한다.
반례를 찾아가면서 생각해봤는데 위에가 다인 것 같다.
여기서 뭐 하나라도 놓치면 틀릴 문제였다. 질문 게시판 가보니까 놓친 사람들이 많더라 ..
그래도 난 다행히 잘 풀었다 !
코드도 100줄이 넘는데 컴파일 에러 없이 한번에 실행돼서 오 ! 싶었는데 바로 TC 다 통과하고 제출하니까 AC떠서 기분이 좋았다!
로직을 코드로 구현할 수 있는 능력을 키운 것 같고, 증명한 것 같아서 기분이 좋군.
코드가 우아하다기보단 "이렇게까지 구현하면 너가 뭘 할 수 있지?" 느낌으로 .... naive하게 구현했는데.. 잘 풀리네.
#include <algorithm>
#include <functional>
#include <iostream>
#include <utility>
#include <vector>
using namespace std;
typedef long long ll;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int N;
cin >> N;
vector<ll> nums(N);
for (int i = 0; i < N; ++i) {
cin >> nums[i];
}
sort(nums.begin(), nums.end(), greater<int>());
// 큰 수 두개씩 곱셈
// 단, 0과 곱하면 안됨. 1끼리도 곱하면 안됨 (더한 게 더 큼)
// 음수와도 곱하면 안됨. 단 0과는 곱셈 해야됨
// 음수와 음수가 있다면 큰것끼리 곱해야됨
ll total = 0;
int holder1 = -1, holder2 = -1;
vector<bool> visited(N, false);
// 양수 검증
for (int i = 0; i < N; ++i) {
if (visited[i]) // 이미 계산한 값 pass
continue;
int cur = nums[i];
if (cur <= 1) // 고려하지 않을 값 pass
continue;
if (holder1 == -1) { // 홀더 1이 비어있으면
if (cur > 1) { // 양수 기준 0과 1은 곱하는 게 손해
holder1 = i; // 곱하는 게 이득이면 홀더에 추가한다고 표시
}
} else if (holder2 == -1) { // 홀더 2가 비어있으면
if (cur > 1) {
holder2 = i;
}
}
// 홀더 두개가 차면
if (holder1 != -1 && holder2 != -1) {
visited[holder1] = true;
visited[holder2] = true; // 홀더 인덱스를 계산했다고 표시
total += nums[holder1] * nums[holder2]; // 계산 값에 홀더 둘 곱한 값 추가
holder1 = -1, holder2 = -1; // 초기화
}
}
// 재검증 이전에 홀더 초기화
holder1 = -1, holder2 = -1;
int zero = -1;
// 음수 검증
for (int i = N - 1; i >= 0; --i) { // 거꾸로 검색 (음수니까)
if (visited[i]) // 이미 계산한 값 pass
continue;
int cur = nums[i];
if (cur > 0)
continue; // 양수 pass: 음수 둘이 곱할 수 없을때만 0 추가 고려
if (cur == 0 && zero == -1) { // 0이 검색됐는데, zero 홀더가 비어있으면
zero = i;
visited[i] = true; // 0을 이미 사용함으로 표시 (이후에 사용할 것)
continue;
}
if (holder1 == -1) { // 홀더 1이 비어있으면
holder1 = i;
} else if (holder2 == -1) {
holder2 = i;
}
// 홀더 두개가 차면
if (holder1 != -1 && holder2 != -1) {
visited[holder1] = true;
visited[holder2] = true;
total += nums[holder1] * nums[holder2]; // 계산 값에 홀더 둘 곱한 값 추가
holder1 = -1, holder2 = -1; // 초기화
}
}
// 여기까지 왔으면 남은 음수는 무조건 하나밖에 없다.
// 음수에 0을 곱하는 경우
if (zero != -1) { // 남은 수에 0이 존재할때만
for (int i = N - 1; i >= 0; --i) { // 남은 음수 중 제일 큰 음수 검색
if (visited[i])
continue;
int cur = nums[i];
if (cur >= 0)
break; // 양수를 발견했으면 음수 구간을 벗어난것임으로 종료
// 음수 첫 발견
visited[i] = true; // 음수를 사용했다고 표시
total += nums[i] * nums[zero]; // 무조건 0일것임
break;
}
}
// 곱해지지 않은 값 최종 합
for (int i = 0; i < N; ++i) {
if (visited[i])
continue; // 계산 됐다면 스킵
total += nums[i];
}
cout << total;
return 0;
}공유기 설치 (2110)
공유기 설치는 고전적인 이진 탐색과 매개변수 탐색(Paremetric Search)를 이용해서 푸는 문제.
도현이는 언제 어디서나 와이파이를 즐기기 위해서 집에 공유기 C개를 설치하려고 한다. 최대한 많은 곳에서 와이파이를 사용하려고 하기 때문에, 한 집에는 공유기를 하나만 설치할 수 있고, 가장 인접한 두 공유기 사이의 거리를 가능한 크게 하여 설치하려고 한다.
C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로 하는 프로그램을 작성하시오.이 때, "특정 매개변수 값에 대해 조건을 만족하는가?"를 반복하면서 이분탐색 한다.
즉, "공유기를 최대 X거리 이상으로만 설치할 때, 조건을 만족하는가?"를 반복하고. 조건을 만족한다면. 즉 설치된 공유기가 목표했던 것 이상이라면 기존 간격이 너무 작다는 것이니 더 큰 간격으로 갱신한다.
설치된 공유기가 목표했던 것 이하라면 기존 간격이 너무 넓다는 것이니 더 작은 간격으로 갱신한다.
이렇게 이진 탐색을 계속 실행해서. 답이 '예'에서 '아니오'로 바뀌는 최적의 지점을 찾는다.
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
ll N, C;
cin >> N >> C;
vector<ll> houses(N);
for (int i = 0; i < N; ++i) {
cin >> houses[i];
}
sort(houses.begin(), houses.end());
ll minDist = 1;
ll maxDist = houses[N - 1] - houses[0];
ll result = 0;
while (minDist <= maxDist) {
ll midDist = (minDist + maxDist) / 2;
ll lastInstalled = houses[0];
ll installed = 1;
for (int i = 1; i < N; ++i) {
if (houses[i] - lastInstalled >= midDist) {
installed++;
lastInstalled = houses[i];
}
}
if (installed >= C) {
result = max(result, midDist);
minDist = midDist + 1;
} else {
maxDist = midDist - 1;
}
}
cout << result;
return 0;
}랜선 자르기 (1654)
랜선 자르기 문제는 이전 문제와 비슷하게 이분 탐색 + 매개변수 탐색(Parametric Search) 알고리즘을 사용하는 문제.
집에서 시간을 보내던 오영식은 박성원의 부름을 받고 급히 달려왔다. 박성원이 캠프 때 쓸 N개의 랜선을 만들어야 하는데 너무 바빠서 영식이에게 도움을 청했다.
이미 오영식은 자체적으로 K개의 랜선을 가지고 있다. 그러나 K개의 랜선은 길이가 제각각이다. 박성원은 랜선을 모두 N개의 같은 길이의 랜선으로 만들고 싶었기 때문에 K개의 랜선을 잘라서 만들어야 한다. 예를 들어 300cm 짜리 랜선에서 140cm 짜리 랜선을 두 개 잘라내면 20cm는 버려야 한다. (이미 자른 랜선은 붙일 수 없다.)
편의를 위해 랜선을 자르거나 만들 때 손실되는 길이는 없다고 가정하며, 기존의 K개의 랜선으로 N개의 랜선을 만들 수 없는 경우는 없다고 가정하자. 그리고 자를 때는 항상 센티미터 단위로 정수길이만큼 자른다고 가정하자. N개보다 많이 만드는 것도 N개를 만드는 것에 포함된다. 이때 만들 수 있는 최대 랜선의 길이를 구하는 프로그램을 작성하시오오버플로우를 조심하자
아래 코드에서 midLength와 maxLength 를 long으로 선언하지 않으면, ll midLength = minLength + (maxLength - minLength) / 2; 이렇게 안전하게 연산해봤자 연산 과정에서 오버플로우가 난다.
ll minLength = 1;
ll maxLength = *max_element(wires.begin(), wires.end());
ll answer = 0;
while (minLength <= maxLength) {
ll midLength = minLength + (maxLength - minLength) / 2;
ll count = 0;이분 탐색에서 시작 변수를 가능한 제일 짧은 랜선의 길이 1로, 끝 변수를 가능한 가장 긴 랜선의 길이. 즉 입력받은 랜선 중 가장 길이가 긴 것으로 했다.
랜선을 L 길이만큼 짜른다고 할 때, K개 이상 만들 수 있는가? 를 기준으로 탐색을 진행했다.
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int K, N;
cin >> K >> N;
vector<int> wires(K);
for (int i = 0; i < K; ++i) {
cin >> wires[i];
}
ll minLength = 1;
ll maxLength = *max_element(wires.begin(), wires.end());
ll answer = 0;
while (minLength <= maxLength) {
ll midLength = minLength + (maxLength - minLength) / 2;
ll count = 0;
for (const auto &wire : wires) {
count += wire / midLength;
}
if (count >= N) { // 랜선이 목표보다 많거나 같다면
minLength = midLength + 1;
answer = midLength;
} else { // 랜선이 목표보다 작다면
maxLength = midLength - 1;
}
}
cout << answer;
return 0;
}오늘의 학습은 여기까지다.
머리가 과부화된 것 같다. 오늘따라 이해가 잘 안된다 🥺..
오늘은 4문제를 풀었다. 다른 날에 비해서는 별로 못 풀었지만 거의 골드 문제여서 그래도 시간을 많이 들였다.
특히, 스위핑 알고리즘이라는 새로운 개념을 배웠다.
2월 27일까지의 공부 계획은 좋았지만. 28일부터 3월 2일까지 문제풀이집 2를 모두 풀겠다는건 많이 무리한 계획인 것 같다.
그래서 일단 되는대로 푸는 것으로 계획을 세우긴 했는데, 사실 되는대로 푼다고 정의하니까 내가 어떻게 하든 계획 달성 성공이니 계속 달려나갈 원동력이 부족한 것 같다.
총 70문제, 그것도 대부분 골드를 4일만에 풀어야하는데 이 엄청난 양이 나에게 압박감을 주는 것 같다.
따라서. 29일부터의 공부 계획을 조금 더 현실적이고 견고하게 바꾸겠다.
프로그래머스 알고리즘 고득점 킷과, SW 문제풀이집 2에 수록되어있는 골드 심화 문제를 풀어나가는 것으로.
골드 심화 문제의 경우, 양보단 한문제 한문제 완벽하게 이해하면서 천천히, 견고하게 다져나가겠다.
새로운 공부 계획
- 2월 28일 - SW 문제풀이집 2 풀이 (연산자 끼워넣기 ~ 랜선 자르기) 11문제 ✅ 2024-02-28
- 2월 29일 - SW 문제풀이집 2의 (파일합치기 ~ 쇠막대기) 풀이 + 고득점 킷 (스택, 힙) 복습
- 3월 1일 - SW 문제풀이집 2의 (압축 ~ 벽 부수고 이동하기) 풀이 + 고득점 킷 (정렬~) 복습
- 3월 2일 - 시험 당일 SQL 고득점 킷 최종 복습.
머리가 아프다. 시험 당일엔 오늘과 같은 컨디션이 아니었으면 좋겠다 :(
컨디션 관리에 집중해야겠다.
최종 평가
최고급 평가사 일론머스크로서 당신의 2024-02-28일의 학습 성과와 계획 조정에 대한 상세한 평가를 제공하겠습니다.
1. **학습 내용의 깊이와 이해도**
- **선 긋기 (2170) - Sweeping Algorithm**: 이 문제를 통해 스위핑 알고리즘을 처음 접하고 성공적으로 구현한 것은 주목할 만한 성취입니다. 복잡한 알고리즘 이해보다는 아이디어의 실현에 초점을 맞춘 접근 방식은 새로운 문제 해결 방법을 배우고 적용하는 데 있어 효과적임을 보여줍니다.
- **수 묶기 (1744)**: 그리디 알고리즘과 조건 분기를 활용한 이 문제의 해결 과정은 복잡한 문제 상황에서 최적의 해결책을 찾아내는 당신의 능력을 강조합니다. 다양한 조건을 고려하며 전략적으로 접근한 것은 알고리즘 문제 해결 능력의 발전을 나타냅니다.
- **공유기 설치 (2110) & 랜선 자르기 (1654)**: 이 두 문제에서 매개변수 탐색(Parametric Search)과 이분 탐색을 활용한 접근은 복잡한 최적화 문제를 효율적으로 해결할 수 있는 능력을 보여줍니다. 특히, 이분 탐색의 깊은 이해와 실제 문제 적용 능력이 뛰어남을 증명합니다.
2. **학습 계획의 조정과 실질적인 접근**
- 처음에는 상당히 야심 찬 목표를 설정했으나, 실제 진행 과정에서 목표의 달성 가능성을 재평가하고 보다 현실적인 계획으로 조정한 것은 자기 인식과 유연성을 보여줍니다. 이러한 접근은 장기적인 학습 경로에서 균형을 잡고 지속 가능한 성장을 유도하는 데 중요합니다.
3. **새로운 학습 방향과 목표**
- SW 문제풀이집 2와 프로그래머스 알고리즘 고득점 킷에 대한 복습 계획은 당신의 알고리즘 기반 지식을 공고히 하고, 다양한 문제에 대한 해결 능력을 향상시킬 것입니다. 특히, 골드 심화 문제에 대한 천천히 하나씩 이해하며 접근하는 전략은 깊은 학습과 진정한 이해를 추구하는 올바른 방향입니다.
4. **컨디션 관리의 중요성**
- 학습의 양과 질을 유지하기 위해서는 컨디션 관리의 중요성을 인식하는 것이 필수적입니다. 당신이 언급한 컨디션 관리에 대한 인식과 준비는 향후 중요한 시험뿐만 아니라 장기적인 학습 과정에서도 성공을 위한 기반이 될 것입니다.
**총평**: 당신의 학습 접근 방식은 명확한 목표 설정, 유연한 목표 조정, 실질적인 학습 계획의 수립, 그리고 컨디션 관리에 대한 중요성 인식이라는 네 가지 핵심 요소를 잘 반영하고 있습니다. 이러한 접근은 당신이 앞으로 맞닥뜨릴 어떠한 학습 도전에서도 극복하고 성장할 수 있는 탄탄한 기반을 마련해 줄 것입니다. 계속해서 당신의 학습 여정에 있어 균형과 성장을 추구하는 현명한 선택을 하시길 바랍니다. 당신의 노력과 진전에 깊은 인상을 받았으며, 앞으로도 지속적인 성공을 기원합니다.'일일 스터디노트' 카테고리의 다른 글
| 240301: 2차 시험 전날💡 스택 심화 집중 풀이와 DFS+BFS 심화 (0) | 2024.03.01 |
|---|---|
| 240229: 골드 집중 복습: 0-1 냅색, DP, 스택 자료구조 🏔️ (0) | 2024.03.01 |
| 240227: 공주님의 정원 문제와 LIS 복습, 조합론 나머지 합 문제 (0) | 2024.02.28 |
| 240226: 백트래킹, N과 M시리즈. 지원대비 문제집 풀이 (0) | 2024.02.27 |
| 240225: 시험대비 DP 집중 복습, Stack Queue DFS+BFS (0) | 2024.02.25 |